首先要理解单调栈：单调栈就是在栈结构的基础上，其内部元素从栈顶到栈底呈单调递增/递减的趋势。
什么时候使用单调栈：通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时就要想到可以用单调栈了。时间复杂度为O(n)。
单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高/低的元素，优点是整个数组只需要遍历一次。
在使用单调栈的时候首先要明确如下几点：
1. 单调栈里存放的元素是什么？
单调栈里只需要存放元素的下标i就可以了，如果需要使用对应的元素，直接T[i]就可以获取。
2. 单调栈里元素是递增呢？ 还是递减呢？
看题目要求，比如求右边第一个比本元素大的就是递增，因为只有递增的时候，栈里要加入一个元素 i 的时候，才知道栈顶元素在数组中右面第一个比栈顶元素大的元素是 i 。
这么说还是有点抽象，具象化的看一道题目吧，Leetcode739.每日温度
看完题目，显然就是找每个元素右边第一个比自己大的元素，那当然可以尝试使用单调栈了。
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int[] res = new int[temperatures.length];
ArrayDeque<Integer> deque = new ArrayDeque<>();
deque.push(0);
for (int i = 1; i < temperatures.length; i++) {
// 遍历元素 > 栈顶元素 : 更新res 弹出栈顶元素 压入遍历元素
if (temperatures[i] > temperatures[deque.peek()]) {
// 多次比较 直至栈内为空
while (!deque.isEmpty() && temperatures[i] > temperatures[deque.peek()]) {
int poll = deque.poll();
res[poll] = i - poll;
}
deque.push(i);
} else {
// 遍历元素 <= 栈顶元素 ： 压入遍历元素 构建单调栈
deque.push(i);
}
}
return res;
}
}
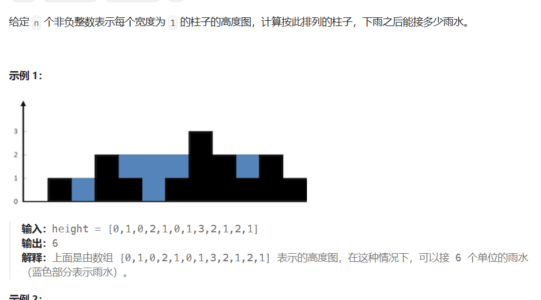
再看一道 hard 级别的题目，非常经典的接雨水，Leetcode42.接雨水
分析完题目以后，发现求的就是当前位置的左侧最大高度和右侧最大高度，再取两者最小来计算雨水高度（木桶效应）。那使用单调栈，就可以同时把左右侧的两个高度记录下来求解了。
class Solution {
public int trap(int[] height) {
int ans = 0;
// 单调递增栈：从栈顶到栈底递增，存放下标
ArrayDeque<Integer> stack = new ArrayDeque<>();
// 遍历元素 去寻找右侧第一个比当前元素高的柱子
for (int i = 0; i < height.length; i++) {
while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
// 此时遍历元素比栈顶元素大 说明找到了凹槽
// 且当前元素i是右边第一个比栈顶元素mid大的柱子
// mid弹出后，此时的栈顶元素是左边第一个比mid大的柱子
int mid = stack.pop();
if (stack.isEmpty()) {
break;
}
// 计算雨水高度：左右柱子高度最小值（木桶效应） - mid高度
int h = Math.min(height[i], height[stack.peek()]) - height[mid];
// 计算宽度
int width = i - stack.peek() - 1;
ans += h * width;
}
// 比栈顶元素小，符合单调递增栈（顶到底递增），直接入栈
stack.push(i);
}
return ans;
}
}