Leetcode96.不同的二叉搜索树

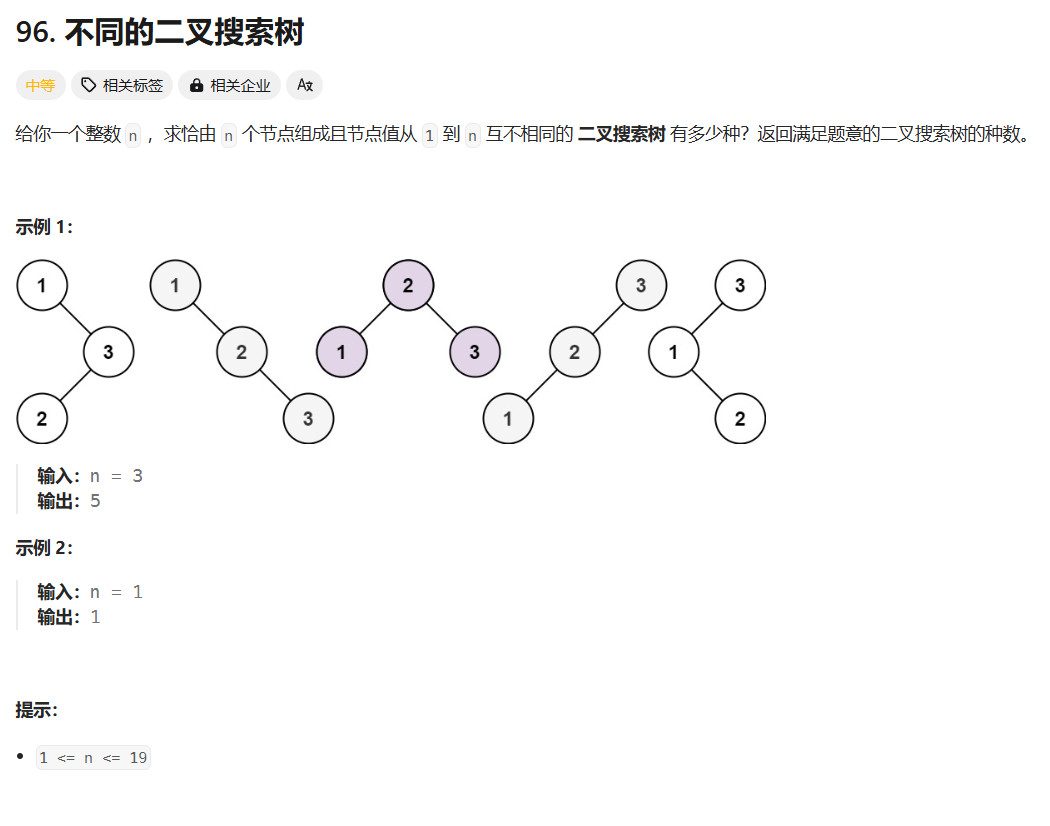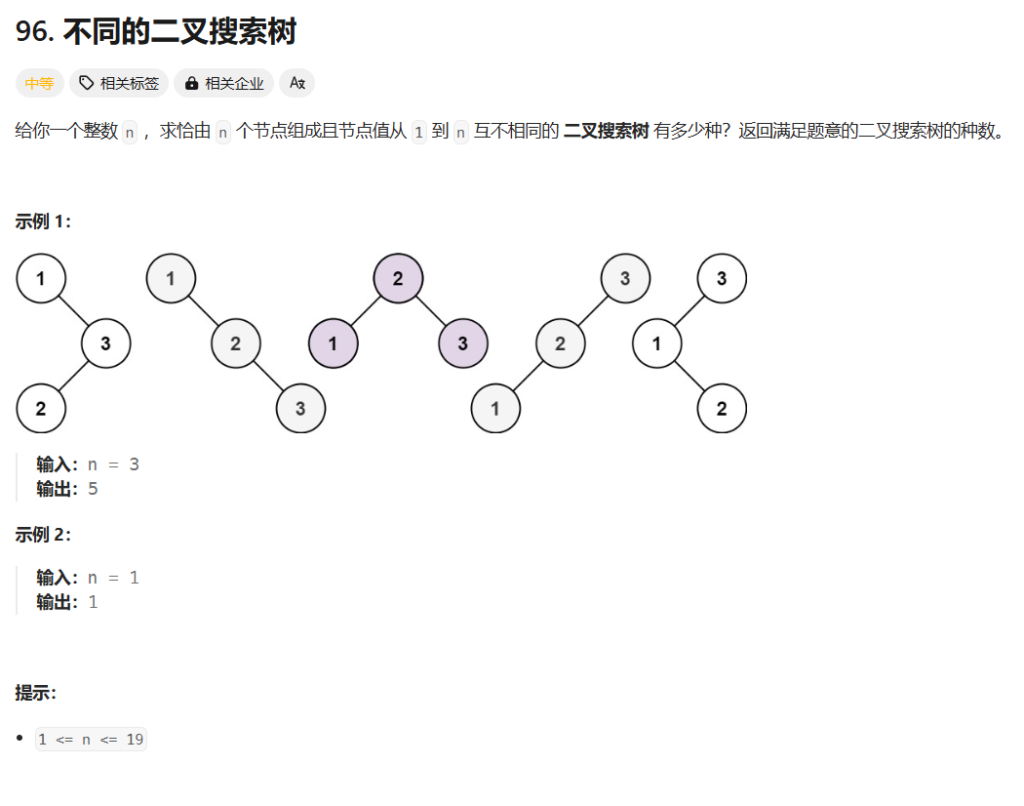
一开始很容易想到根据 n 的值去找规律，联想到使用动态规划，但是发现规律很难找，甚至普通规律找不出来。

1. 确定 dp 数组的含义：i 个节点有 dp[i] 种不同的二叉搜索树

2. 确定递推公式：

先看看 i 为 1 和 2 的情况吧：

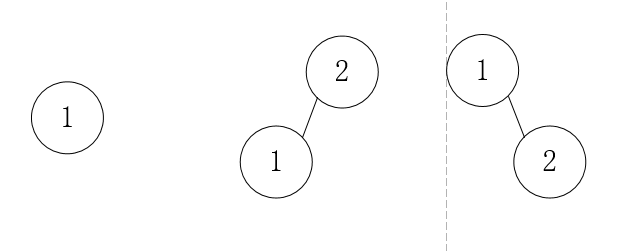
i 为 3 时，我们根据头节点的值来分开看（图片出处：代码随想录)：

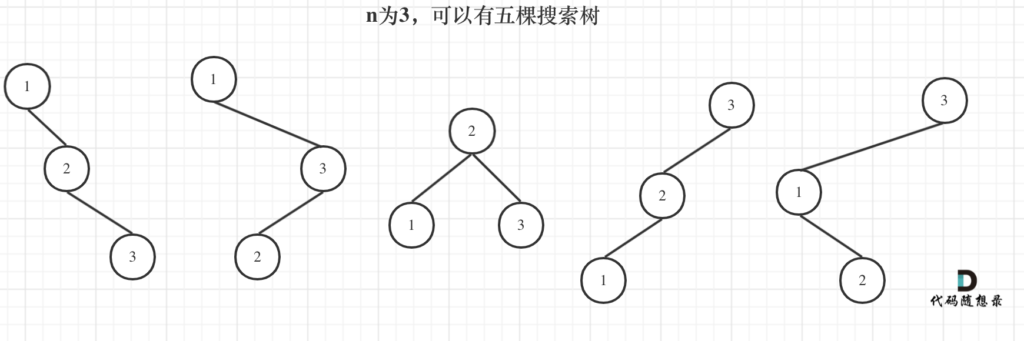
我们可以发现，头节点为 1 和 3 时，他的所有子树形状和 i = 2 时的全部树形状完全一样；头节点为 2 时，他的子树形状和 i = 1 时的数形状一样。

于是我们可能有点眉目了，dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量。

元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量

元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量

元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量

所以很容易得到 dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

根据这个公式，我们可以联想到遍历加和，于是 dp[i] += dp[j – 1] * dp[i – j]， j-1 是以 j 为头结点左子树节点数量，i-j 是以j为头结点右子树节点数量

3. 初始化 ：

根据递推公式，我们肯定要知道 dp[0] 的值，可以想到，空节点其实也是二叉搜索树，所以 dp[0] = 1。另外，从乘积角度考虑，dp[0] 总不能为 0 吧。

4. 确定遍历顺序 ：

从递推公式 dp[i] += dp[j – 1] * dp[i – j] 看出，dp[i] 依靠之前节点的状态，所以顺序是从前向后。

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= i; j++) {
        dp[i] += dp[j-1] * dp[i-j];
    }
}

5. 举例推导dp数组：这个根据用例测试看一看就行，也很难去自己写出来

给出完整代码：

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];  // i个节点有dp[i]种不同的二叉搜索树
        // dp[i] += dp[j - 1] * dp[i - j]
        // j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量
        dp[0] = 1;  // 空节点也是一颗二叉搜索树
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j-1] * dp[i-j];
            }
        }
        return dp[n];
    }
}

总结一下，这道题虽然是中等难度，但难度直逼hard，规律不好找，找不到规律递推公式更是gg，还是要多练。